|
Size

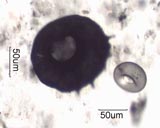
Size is a far more complex issue than might seem to be the case. In the
fireweed pollen grain above, five different sizes are shown. The size
of the largest enclosed circle is [1], 53.6um. The size of the smallest
enclosing circle is [2], 94.2um. The longest dimension is [3], 91.9um.
[4], 72.6um, is the Martin's diameter and one of the Ferret's diameters.
There are many other sizes that could be calculated for this particle.
Size is simple for a circle, but quickly becomes more difficult as the aspect
ratio increases or the length of the perimeter significantly exceeds
the perimeter of the enclosed circle. There are a number of standard
approaches. If bridging is a concern then the longest dimension of the
particle
is its size. If the concern is a sieve size then the larger of the two
smallest dimensions is the size. The average of 6 or more Ferrets is another
standard measure. Other measures include the diameter of the enclosing
circle, the diameter of the enclosed circle, the projected intercept with a
line at a fixed angle, aerodynamic equivalent diameter, diameter of a circle
with the same area, diameter of a circle with the same perimter, and more.
. . . Circular Particles


. . . Equant
Dimensions appear similiar
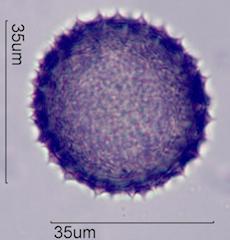
. . . Equivalent Circular Area Diameter
Particle Area = .25(pie)(d2) or 32.9um for the particle below.
. . . Equivalent Circular Perimeter Diameter
Particle Perimeter = (pie)(d) or 43.9um for the particle below.

. . . Aerodynamic Equivalent Diameter
Equivalent Spherical Volume Diameter (30.43um) times (Equivalent Circular
Area Diameter (32.9) divided by Equivalent Circular Perimeter Diameter
(43.9))
or (30.43)(32.9/43.9) = 22.8um

. . . Sieve Equivalent
The diameter of the largest enclosed circle. If the hieght above the slide is
concidered the smallest diameter then two of the particle's
dimensions are at or below this size. The two smallest dimensions determine
size of the mesh that the particle will pass through.

. . . Longest Dimension: Bridging Path Equivalent
The diameter of the smallest enclosing circle or longest dimension.

. . . Shortest Dimension
The Diameter of the Largest Enclosed Circle: Shortest Dimension.

|