|
Roundness
One simple deffinition of roundness is the maximum ferret minus the minimum
ferret of the particle. For a circle this is equal to "0".
Another measure is the projected area of the particle divided by the area of
the smallest enclosing (circumscribing) circle. A perfect
circle would result in a value of "1". The sum of all the inclosed radii for
each corner on a particle divided by the number of corners
(the average radius for the sum of radii for all corners) divided by the
radius of the maximum enclosed circle can result in a number of
shapes being equal to a circle though they don't look like a circle. They
would be neccessarily rounded. There are a number of other
ways to calculate a value for roundness. The six subjective classes
generally suffice but some measurements are provided below.
. . . Maximum Enclosed Circle Radius/Minimum Circumscribed Circle Radius

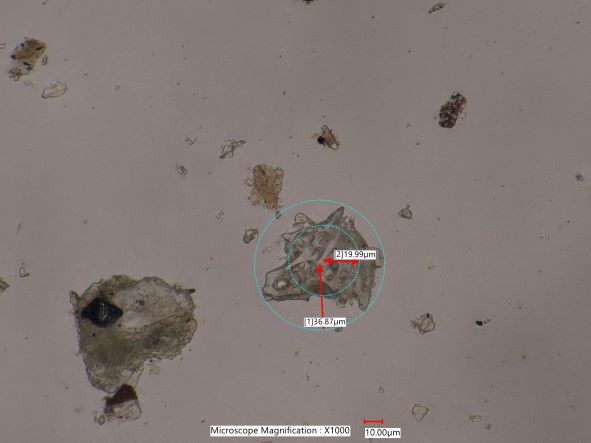
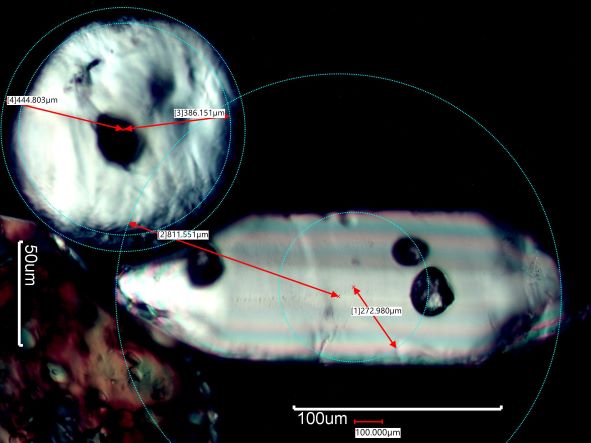
VALUES. . . 0.61 . . . . . . . . . . . . . . 0.27 . . . . . . . . . . . . 0.82
and 0.34 . . . . . . . . . . 0.54
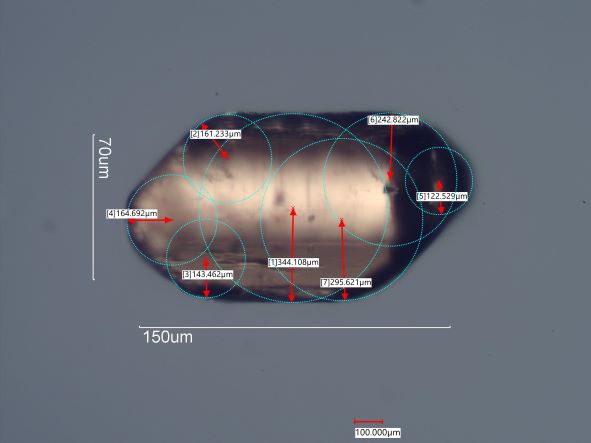
. . . Average Corner Radius/Maximum Enclosed Circle Radius


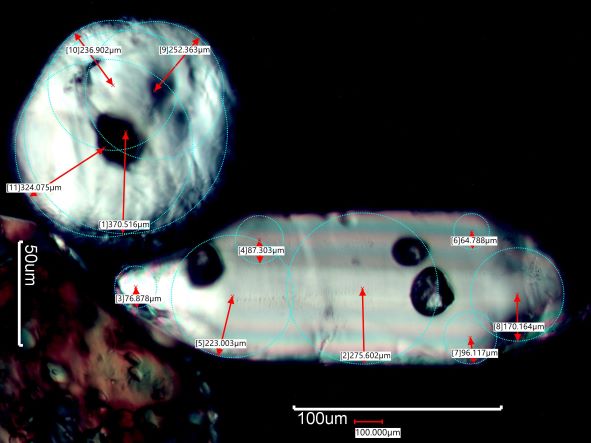

VALUES. . . 0.17 . . . . . . . . . . . . . . 0.13 . . . . . . . . . . . . 0.73
and 0.43 . . . . . . . . . . 0.55
|