|
Symmetry
Symmetry through the microscope tends to be reduced to two dimensional
symmetries. There are basically two classes of symmetries. There
are rotational symmetries and organizational symmetries. Crystals and
regular geometric forms have symmetries where on one or two axis
rotations the positoions are indistiguishable. these include two-fold,
three-fold, four-fold, five-fold, six-fold, mirror, and point
symmetries. Many life-forms have symmetries where a part is approximately
mirrored by other parts of the structure. Leaves are a common example.
one side is duplicated on the other side across from it. This is not a
rotational symmetry. Rotating the leaf on its symmetry axis would first
exchange the top of the leaf with the bottom of the leaf, which is not
equivalent. It is a type of approximate mirror symmetry.
The symmetries detected may help identify a crystal system or a life form.
. . . Mirror Symmetry

. . . Two-Fold or Bisymmetry
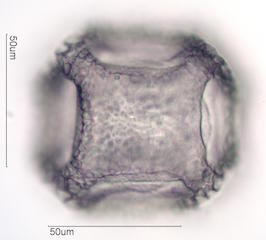
A cube has has 4 two-fold axes. A rectangle has 2 two-fold axes. These are
rotation symmetries. Many life forms are bisymmetric. They critically have a
one
fold axis where right and left sides are approximately duplicated. A pinate
diatom may have as many as three bifold symmetries.
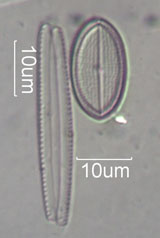

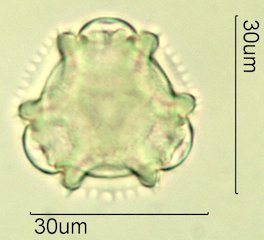
. . . Three-Fold Symmetry

. . . Four-Fold Symmetry
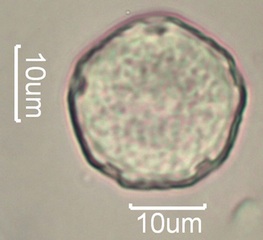
. . . Five-Fold Symmetry
. . . Six-Fold Symmetry

. . . Mirror Symmetry
. . . Point Symmetry
|