|
Interface Properties
Features evident at the interface between the particle and the adjacent
medium.
Relative Refractive Index
The relative refractive index referes to the difference in the real part of
the refractive index, "n" of the particle minus "n" of
the medium (npart - nmedium). The greater the difference, either positive or
negative, the darker the bondary of the particle. This is presented in
more detail under "Relief".
Relative Absorption
Relative Absorption (kpart - kmedium): The refractive index is a complex
number having both a real and an imaginary parts.
The imaginary part is the absorption coefficient and is designated as "k".
The higher the imaginary part of the refractive index the
darker the particle.
Relief
Relief, simply speaking, is the contrast at the edge of a particle as a
result of differences in the refractive index between the particle
and the mounting medium. John Delly provides a more detailed definition in
his book, ESSENTIALS OF POLARIZED LIGHT MICROSCOPY AND ANCILLARY
TECHNIQUES. His definition is "Contrast between a specimen and its
surroundings (typically mounting media) due to the difference between
their refractive indices. The greater the numerical difference in refractive
indices, the stronger the relief. Expressed as positive or
negative; high, medium, or low."
. . . Glass Fiber and Silica Phytoliths in 1.485 refractive index
mounting medium
The first image shows a glass fiber from an office ceiling acoustic tile. The
refractive index of the glass fiber is about 1.520.
The relief is moderate. The sign cannot be determined, positive or negative,
from this image. If it were negative, refractive index
lower than the mounting medium, then the fiber would become dark when the
stage is lowered (bright Becke line out). If it were positive,
refractive index higher than the mounting medium, then the fiber would
become bright when the stage is lowered (bright Becke line in).

This image shows a glass fiber (lower left) and a silica phytolith (upper
right) with oblique illumination. The light is coming in
from the right. The silica phytolith has a lower refractive index, relief is
negative, and so is bright on the right. The glass fiber has a higher
refractive index, relief is positive, and is dark on the right side. With
oblique illumination the relative refractive index can be
determined without having to defocus the particle.

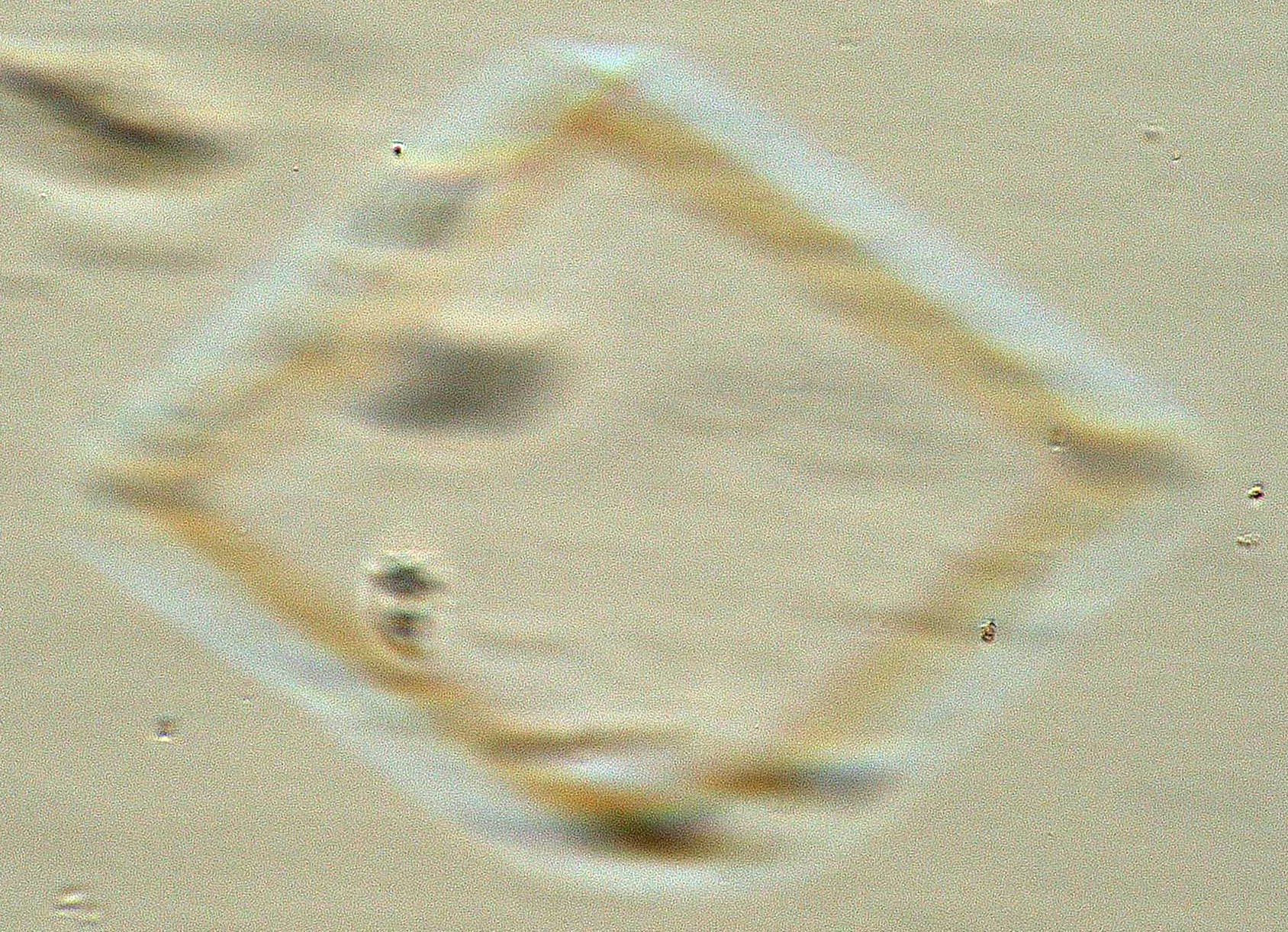
. . . Calcite
Calcite has an omega refractive index of 1.658 or higher (in this case 1.669)
and an epsilon prime refractive index in this orientation
of about 1.550. The first image shows the relief created when a linear
polarizer is oriented to show epsilon prime. The refractive index
difference is 0.114. The result is high relief. The second image is with the
crystal rotated 90 degrees, showing the omega refractive index.
The difference is 0.005 refractive index units. The result is low relief. In
this position, lowering the stage results in a orange Becke' line moving
into the particle and an blue Becke' line moving out, as shown in the third
image. If Oblique illumination is used the dispersion
staining colors are evident on oposite sides of the crystal.



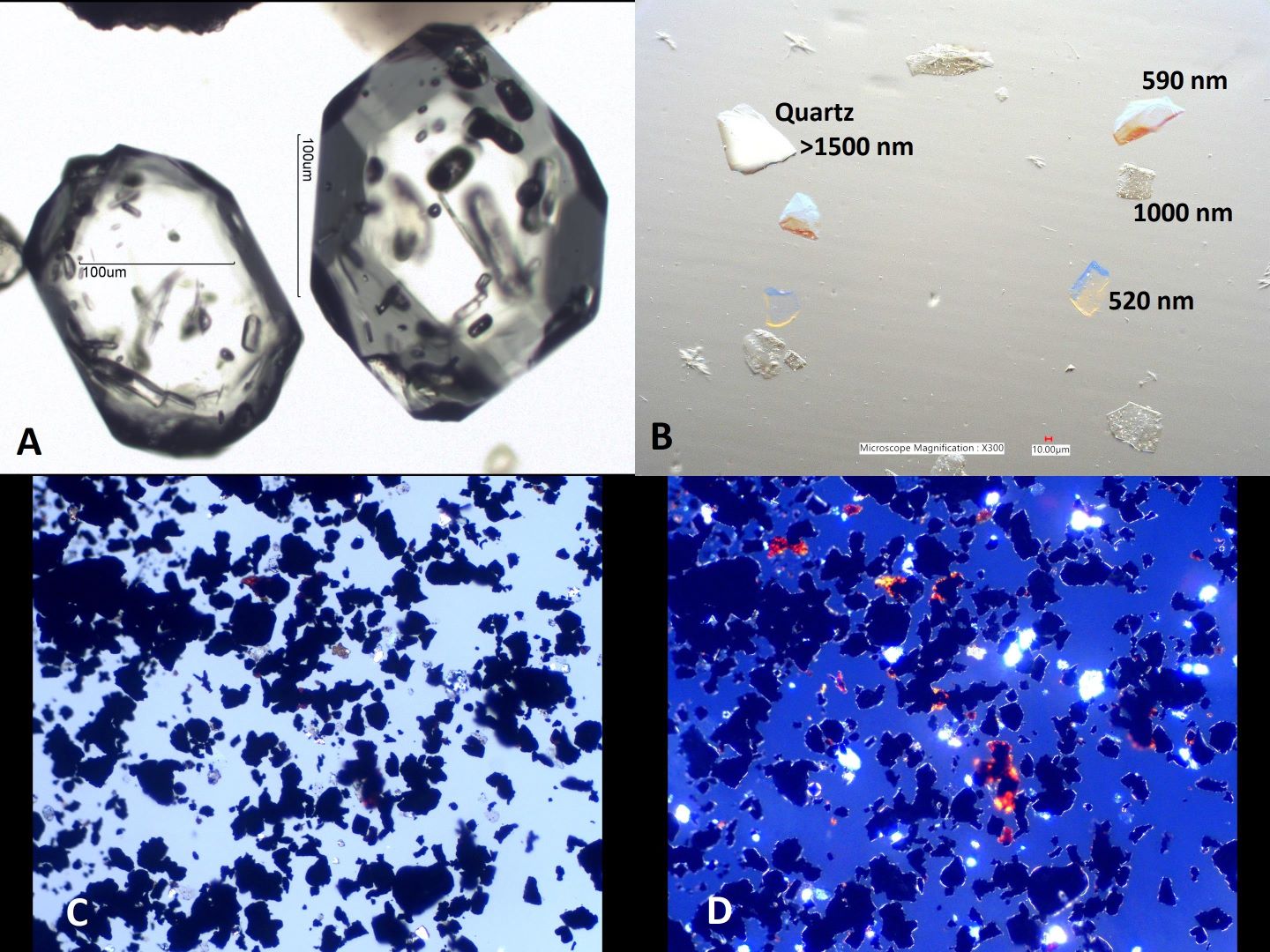
. . . Calcite and Glass Standards in 1.664
The optical glasses have a refractive index of 1.64, 1.66, and 1.67. The
first image shows the calcite crystal in high relief and the
1.67 refractive index glass in low relief. The 1.66 refractive index glass
is invisible. With oblique illumination, the second image,
the optical glasses show dispersion staining colors.


. . . Olivine and Quartz in 1.664 Refractive index Medium
The first image shows the olivine (upper left) and quartz (lower center) in
slightly off crossed polarized light.
The second image is taken with oblique illumination and a single
linear polarizing filter oriented parallel to the high refractive
index of the olivine particle. The quartz is showing high negative relief.
It is bright on the side of the light source and dark on
the other side. That indicates that the refractive indices of the quartz
(1.544 and 1.553) are well below 1.664. The high refractive
index of the olivine particle is about 1.668, based on the dispersion colors
shown.
The third image shows the particles with the linear polarizer rotated
90 degrees. The relief of the quartz particle has not
changed. The olivine particle is now showing its low refractive index of
about 1.656. It is now showing low negative relief because
its refractive index in this position is slightly lower than the 1.664 of
the mounting medium.



Dispertion Staining
. . . Dispertion Staining Color Charts
Dispersion Staining Color Charts are approximations of the colors shown by a
particles that matches the refractive index of the mounting
medium at a specific wavelegnth in the visible part of the electromagnetic
spectrum. The colors vary slightly in the real world as a
result of the size and shape of the particle, the type of dispertion
staining used, and the physical configuration and design of the microscope.


. . . Dispertion Staining Standards
This section shows Cargille Standard Optical Glasses in Standard Cargille
High Dispersion Refractive Index Liquids. The intent is to
demonstrate the effects of size and of different microscope configurations
on the colors.
Rotation of Polarization
If the refractive index of a transparent particle is much different than the
medium in contact with it, then the polarized beam can be
changed at the interface as a result of reflection. If the interface is
aligned with the polarizer or analyzer then the beam is not
affected. In other orientations reflection at the interface results in
rotation of the polarized beam and the interface appears to show
a first order white interference color.

Diffraction Effects
Oblique Properties
Interface Kerr Effect?
Polarized light is depolarized at the interface between a conductive particle
and a non-conductive mounting medium. This light halo effect with
transmitted crossed polarized light indicates an opaque particle is a wear
metal particle or at least is conductive. Graphite is sufficiently
conductive
to produce this effect. Pencil debris can be distinguished from combustion
residue by this effect.
. . . . . . Fretting Metal Wear



. . . . . . Graphite



. . . . . . Magnetite Spheres

Diffraction
Fine structure can act as a diffraction grating.
Reflection
Reflection at an interface is a function of the difference in the real part
of the refractive index between the particle and the medium.
Contrast Enhancement
There are literally hundreds of ways to enhance contrast at the edge of a
particle. Simply using crossed polarized light for birefringent
partices is one example. Phase contrast and any of the other hundreds of
interference methods are examples. Rhineberg filters and darkfield
illumination are two more examples. Selecting a contrasting refractive index
mounting medium is an important consideration in desiding whether
the surface features or interial structuctures of the particles are of
interest. A few of those methods are shown here.
. . . Selection of Mounting Medium
If the mounting medium is near the refractive index of the particle then any
internal materials with a different refractive index or bondaries
become more easily visible. Surface features become less apparent. if a
mounting medium with a very different refractive index is selected, then
surface features become easy to visuallize.
. . . Reduced Substage Iris
Reducing the angle of the cone of light impinging on the particle increases
contrast but decreases resolution.
. . . Oblique Illumination
Oblique illumination increases resolution normal the the axis of the
illuminating beam but decreases the resolution for structures parallel to
the projection of the axis on the stage. It also distorts the image to some
extent, exagerating the shape of the particle perpedicular to the
axis of the illuminating beam.
. . . Darkfield Illumination
Darkfield illumination makes all particles, even opaque particles, bright on
a dark field of view. This is an advantage for automated particle
counts and particle obscuration measurements. Resolution is increased.
. . . Rheinberg Filters
Rheinberg filters can create color contrast and can be used to balance
brightness for the objects in the field of view relative to the background.
. . . Other Substage Stops
Modifying the shape or the angle of the illuminating beam relative to the
optic axis of the microscope can create a number of different effects.
. . . Polarized Light
Anisotropic particles become easily visible when crossed linear polarized
light is used, dependent on the orientation of the particle. If
circular polarized light is used then the contrast is no longer dependent on
orientation.


. . . Phase Contrast
Phase contrast is best used with particles that have low contrast when viewed
with brightfield illumination. Phase contrast can be positive
or negative and have a variety of other characteristics that may better suit
a specific application.
. . . Interference Systems
Nomarski, Jamin-Lebedeff, Mach-Zehnder, Hoffman, and many other systems that
alter the diffraction beam path to bring it into
interference with the image beam path create contrast. Many of these systems
can be used quanitatively to measure a few nanometers
difference in pathlengths.
|