|
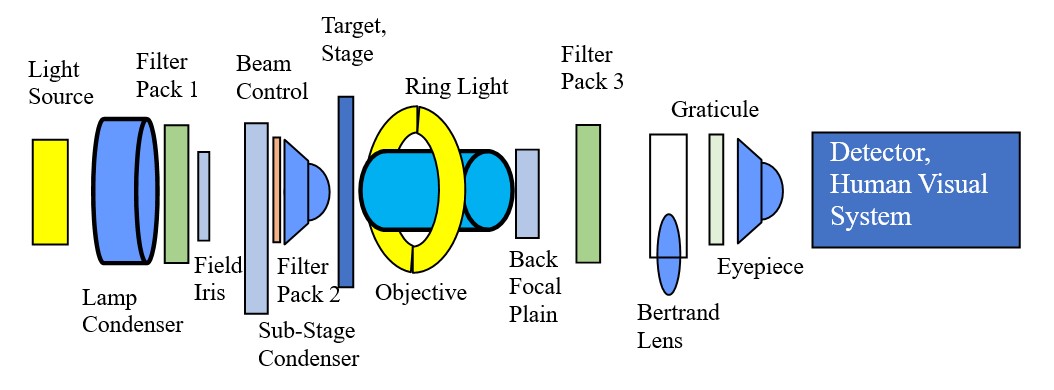
The Light Microscope as an Optical Bench
Morphological Properties
Features evident with transmitted brightfield, oblique, darkfield, or
reflected brightfield, darkfield, oblique, or grazing incident illumination.
. . . Projected Shape
The projected shape of a particle is its transmitted light outline. These
shapes can be very helpful in determining the type of particle
present. Fibers are an obvious example. The shape alone eliminates a huge
range of possibilities. One of the first steps in keying out a
pollen grain is to classify its outline. Shape, as used here, is distinct
from angularity or roundness. Those are details handled later in
this section.
. . . Fibers



. . . Circles
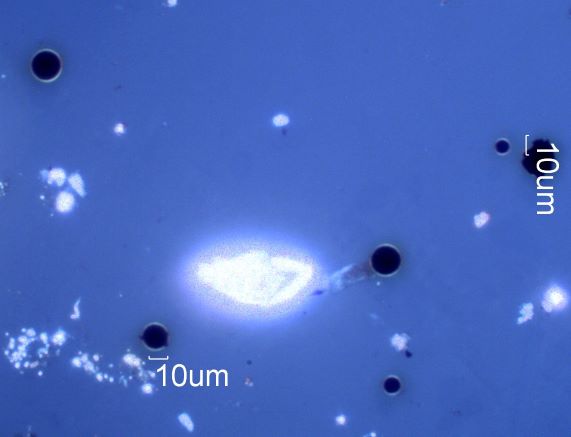
Circles may be the result of a liquid deposition or a growth pattern. The
projected shape is not sufficient to determine if the particle is
spherical.
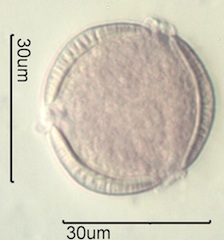

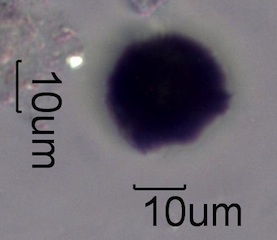
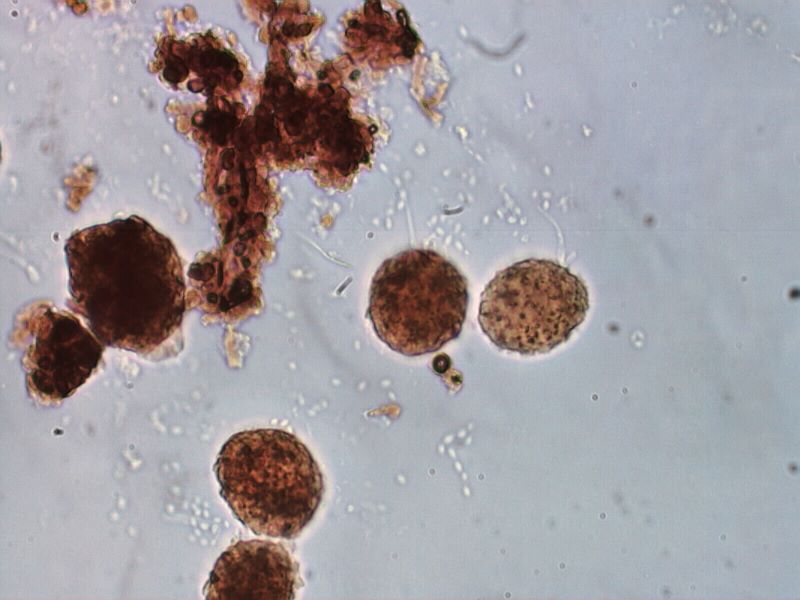
. . . Pollens
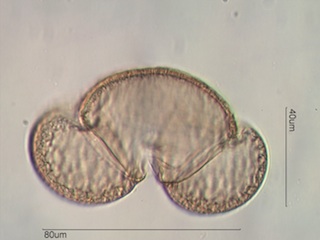
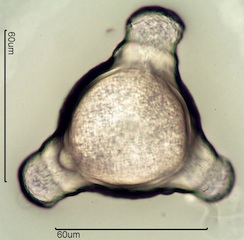
Pollens come in many shapes and vary in size from a few micrometers to
hundreds of micrometers. Most are in the range of 15 to 100 micrometers.
The wall of a pollen grain consists of at least two distinct layers and as
many as four distinct layers that may be separated by characteristic pillar
structures.

. . . Spores
Spores come in many shapes but tend to be smaller than most pollens, often
have a visible attachment point, and a single layer membrane wall.
. . . Diatoms
Diatoms can be divided into two broad types, Pennate and Centric, though
there are also intermediate shapes. Pennate diatoms are elongated, have
one axis much longer than the other two. Centric diatoms have one shorter
axis and the other two are similar giving the diatom a circular or slightly
ellipsoidal shape.
. . . Tapered Cylinders
Tapered cylinders are created by a unidirectional force. In the case of tire
wear it is the friction of the tire against the road. In the case
of some combustion sources it is the shrinkage created by the advancing
thermal gradient.
. . . Globular
Globular particles are particles with internal and external centers of
curvature over their surface.
. . . Straight Edges
Straight edges indicate a linear structural element that may be a cleavage
surface, a growth pattern or a linear force that generated the particle.
. . . Rosettes
Rosettes are the result of growth outward from a central nucleation point.

. . . Dendrites
Dendrites are branching structures were the truck and the branches have the
same diameter. These are common as a result of electrostatic
deposition, some chemical reactions, and some skeletal crystal growth
habits.
. . . Reflected Shape
Reflected darkfield illumination revels three dimensional aspects of a
particles shape not evident with transmitted light. The magnetite
particles below are an example. Charred biomass is another good example.
Without reflected darkfield the identity of these opaque particles
is in question.






. . . Size
Size is a far more complex issue than might seem to be the case. It is simple
for a circle, but quickly becomes more difficult as the
aspect ratio increases or the length of the perimeter significantly exceeds
the perimeter of the enclosed circle. There are a number of
standard approaches. If bridging is a concern then the longest dimension of
the particle is its size. If the concern is a sieve size then
then the larger of the two smallest dimensions is the size. The average of 6
or more Ferrets is another standard measure. Other measures
include the diameter of the enclosing circle, the diameter of the enclosed
circle, The projected intercept with a line at a fixed angle, .
. . . . . . Circles


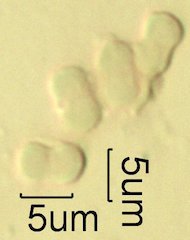
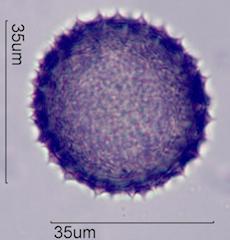
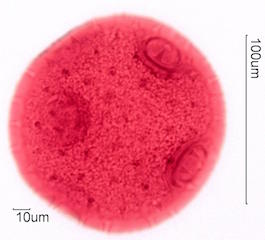
. . . Aspect Ratio, Length/Width
. . . Angles
. . . Angularity
. . . Surface Texture
. . . Internal Texture
. . . Transmitted Scatter
. . . Reflected Scatter
. . . Surface Features
. . . Internal Features
. . . Cross-Section
. . . Mixed Phase Structure
. . . Symmetry
Physiochemical Properties
Features evident as a result of chemical composition, crystallography, or
special arangment of molecules, ions, electron bond features, or excitation
effects that can be made visible. Illumination systems include polarized
light,
phase contrast, interference systems, fluorescence, etc.
. . . Transmission
. . . Absorption
Absorption is the light lost in the particle that is converted from
electromagnetic energy into thermal energy. Absorption
is often wavelength dependent and contributes to the apparent color of the
particle.
. . . . . . Hemetite
Hematite has a complex refractive index of 2.937 + i(0.24268) for epsilon.
The omega refractive index is about 3.2 + i(0.1) at the same wavelength.
When using transmitted light hematite appears nearly opaque. With its high
birefringence, approximately 0.28, even small particles appear red between
crossed polarizing filters. It appears red because it transmits red
wavelengths much more efficiently than the shorter wavelengths (blue, green,
yellow).
With Brightfield illumination the background is too bright to see the small
amount of red light transmitted. With crossed polarizers the
background is dark and the light transmitted as a result of the high
birefringence of hematite is red.




. . . . . . Tourmaline
Polished sections of tourmaline were the first linear polarizing filters.




. . . Reflectivity
. . . Transmission Color
. . . Reflected Color
. . . Birefringence
Birefringence is the property of showing more than one refractive index as a
function of particle orientation and wavelength.
Such a particle will exhibit interference colors when viewed between crossed
circular polarized filters. They will typically show
extinction positions (see below) with rotation of the stage when viewed
between crossed linear polarizing filters.
. . . . . . Low Birefringence
. . . . . . Moderate Birefringence
. . . . . . High Birefringence
. . . . . . Anomalous Birefringence
Anomalous birefringence is the result of birefringence varying by wavelength.
The result is anomalous interference colors. Silicon
carbide and crocidolite asbestos are two common examples. Crocidolite has
higher birefringence in red light (longer Wavelengths) than in
blue. As a result, very thin fibers of crocidolite appear red between
crossed polarizing filters. Thicker fibers appear blue because of
the strong blue color of the mineral.


Silicon carbide has higher birefringence in blue light (Shorter Wavelenghts)
than in red. As a result, blue wavelengths cycle more
rapidly than red wavelengths. Yellow interference color begins for thinner
particles and first order red appears purple because blue
is increasing well before red significantly decreases. This effect changes
the color sequence through the whole range of microscopic
silicon carbide particles.


. . . . . . Stress Birefringence
When a material is placed under stress the distribution of the electrons in
the material is changed. The amount of change is different for each
material and is a characteristic of the material. The photoelastic constant
of the matrial is a measure of the electron displacement (strain) as a
function of the load (stress) applied as long as the deformation is elastic,
springs back when the load is removed. If the Young's Modulus of the
matrial is exceeded, then some of the deformation becomes permenant. In some
materials the applied load can be "frozen" in place, as in the case of
high stress glass sheet. Polarized light can make the displacement visible.
Both plastic deformation and elastic deformation result in an
anisotropic distribution of electrons in the material that becomes visible
as interference colors when the object is viewed between crossed linear or
crossed circular polarizing filters. Click on the photographs below for more
information.
. . . . . . . . . Stress Birefringence in Skin Cells


. . . . . . . . . Stress Birefringence in Safety Glass

. . . . . . Conductivity Birefringence (Hall Effect?)
Polarized light is depolarized at the interface between a conductive particle
and a non-conductive mounting medium. This light halo effect with
transmitted crossed polarized light indicates an opaque particle is a wear
metal particle or at least is conductive. Graphite is sufficiently
conductive
to produce this effect. Pencil debris can be distinguished from combustion
residue by this effect.
. . . . . . . . . Fretting Metal Wear



. . . . . . . . . Graphite



. . . . . . . . . Magnetite Spheres

. . . . . . Form Birefringence
. . . . . . False Birefringence
If the refractive index of a transparent particle is much different than the
medium in contact with it, then the polarized beam can be
changed at the interface as a result of reflection. If the interface is
aligned with the polarizer or analyzer then the beam is not
affected. In other orientations reflection at the interface results in
rotation of the polarized beam and the interface appears to show
a first order white interference color.

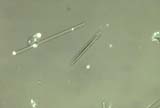
. . . Bireflectivity
. . . Pleochroism
Pleochrism is the property of changing color on rotation when viewed with
linear polarized light. Many colored materials show this property.
. . . . . . Crocidolite

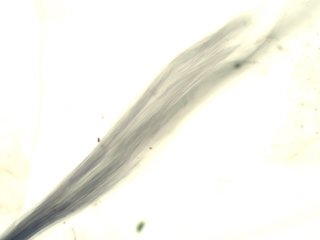
. . . . . . Hornblende




. . . . . . Tourmaline






. . . . . . Olivine



. . . Interference Colors
Interference colors may result from birefringence or from thin film effects.
. . . . . . Thin Film Interference Colors



. . . . . . Birefringence Interference Colors



. . . Twinning
. . . Extinction
. . . Interference Pattern
. . . Fluorescence
Interface Properties
Features evident at the interface between the particle and the adjacent
medium.
. . . Relief
Relief, simply speaking, is the contrast at the edge of a particle as a
result of differences in the refractive index between the particle
and the mounting medium. John Delly provides a more detailed definition in
his book, ESSENTIALS OF POLARIZED LIGHT MICROSCOPY AND ANCILLARY
TECHNIQUES. His definition is "Contrast between a specimen and its
surroundings (typically mounting media) due to the difference between
their refractive indices. The greater the numerical difference in refractive
indices, the stronger the relief. Expressed as positive or
negative; high, medium, or low."
. . . . . . Glass Fiber and Silica Phytoliths in 1.485 refractive index
mounting medium
The first image shows a glass fiber from an office ceiling acoustic tile. The
refractive index of the glass fiber is about 1.520.
The relief is moderate. The sign cannot be determined, positive or negative,
from this image. If it were negative, refractive index
lower than the mounting medium, then the fiber would become dark when the
stage is lowered (bright Becke line out). If it were positive,
refractive index higher than the mounting medium, then the fiber would
become bright when the stage is lowered (bright Becke line in).

This image shows a glass fiber (lowere left) and a silica phytolith (upper
right) with oblique illumination. The light is coming in
from the right. The silica phytolith has a lower refractive index, relief is
negative, and so is bright on the right. The glass fiber has a higher
refractive index, relief is positive, and is dark on the right side. With
oblique illumination the relative refractive index can be
determined without having to defocus the particle.

. . . . . . Calcite
Calcite has an omega refractive index of 1.658 or higher (in this case 1.669)
and an epsilon prime refractive index in this orientation
of about 1.550. The first image shows the relief created when a linear
polarizer is oriented to show epsilon prime. The refractive index
difference is 0.114. The result is high relief. The second image is with the
crystal rotated 90 degrees, showing the omega refractive index.
The difference is 0.005 refractive index units. The result is low relief. In
this position, lowering the stage results in a orange Becke' line moving
into the particle and an blue Becke' line moving out, as shown in the third
image. If Oblique illumination is used the dispersion
staining colors are evident on oposite sides of the crystal.


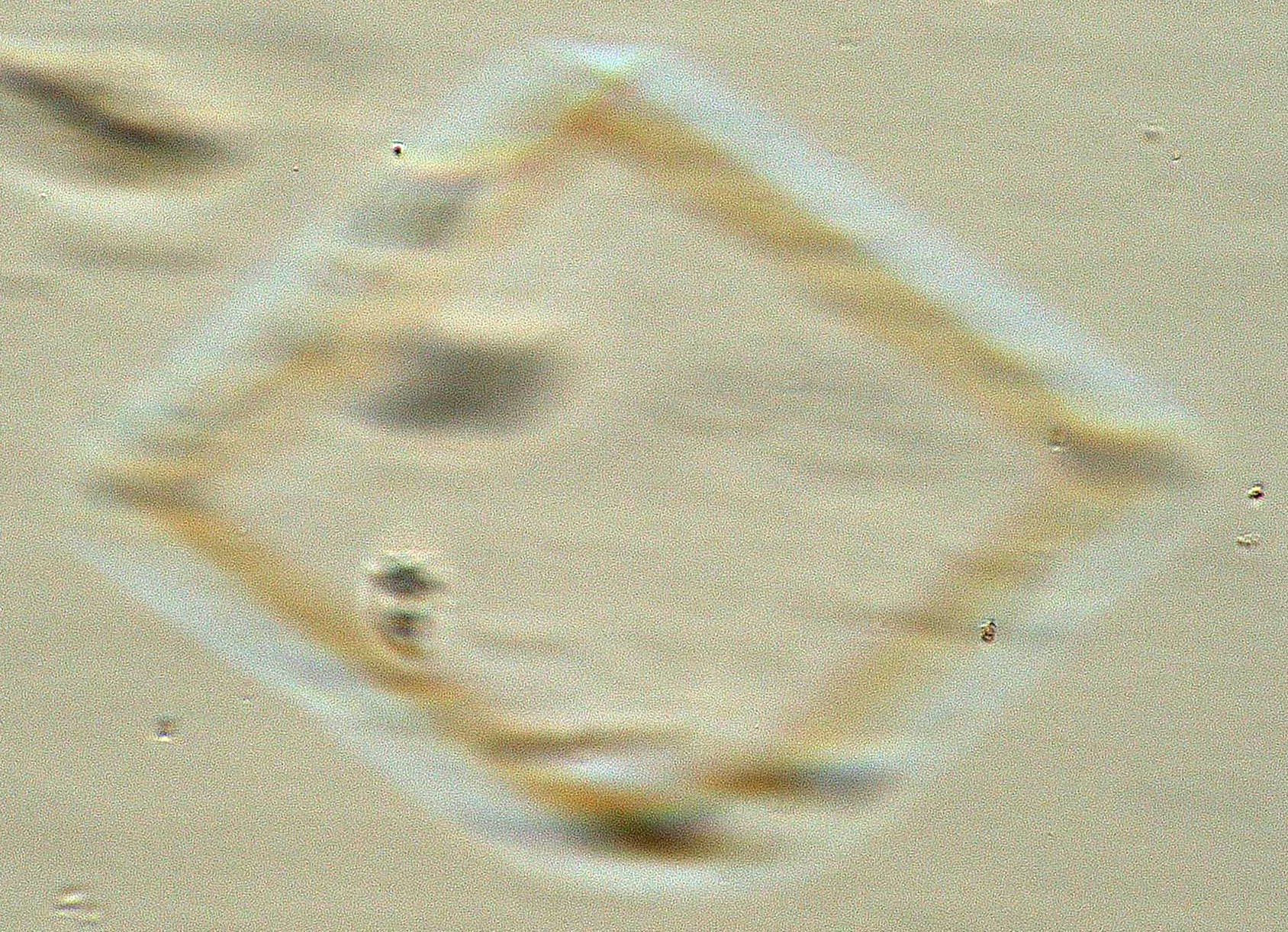

. . . . . . Calcite and Glass Standards in 1.664
The optical glasses have a refractive index of 1.64, 1.66, and 1.67. The
first image shows the calcite crystal in high relief and the
1.67 refractive index glass in low relief. The 1.66 refractive index glass
is invisible. With oblique illumination, the second image,
the optical glasses show dispersion staining colors.


. . . . . . Olivine and Quartz in 1.664 Refractive index Medium
The first image shows the olivine (upper left) and quartz (lower center) in
slightly off crossed polarized light.
The second image is taken with oblique illumination and a single
linear polarizing filter oriented parallel to the high refractive
index of the olivine particle. The quartz is showing high negative relief.
It is bright on the side of the light source and dark on
the other side. That indicates that the refractive indices of the quartz
(1.544 and 1.553) are well below 1.664. The high refractive
index of the olivine particle is about 1.668, based on the dispersion colors
shown.
The third image shows the particles with the linear polarizer rotated
90 degrees. The relief of the quartz particle has not
changed. The olivine particle is now showing its low refractive index of
about 1.656. It is now showing low negative relief because
its refractive index in this position is slightly lower than the 1.664 of
the mounting medium.



. . . Relative Refractive Index
. . . Relative Absorption
. . . Dispertion Staining
. . . . . . Dispertion Staining Color Charts
Dispersion Staining Color Charts are approximations of the colors shown by a
particles that matches the refractive index of the mounting
medium at a specific wavelegnth in the visible part of the electromagnetic
spectrum. The colors vary slightly in the real world as a
result of the size and shape of the particle, the type of dispertion
staining used, and the physical configuration and design of the microscope.


. . . . . . Dispertion Staining Standards
This section shows Cargille Standard Optical Glasses in Standard Cargille
High Dispersion Refractive Index Liquids. The intent is to
demonstrate the effects of size and of different microscope configurations
on the colors.
. . . Rotation of Polarization
If the refractive index of a transparent particle is much different than the
medium in contact with it, then the polarized beam can be
changed at the interface as a result of reflection. If the interface is
aligned with the polarizer or analyzer then the beam is not
affected. In other orientations reflection at the interface results in
rotation of the polarized beam and the interface appears to show
a first order white interference color.


. . . Diffraction Effects
. . . Oblique Properties
|